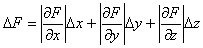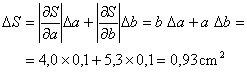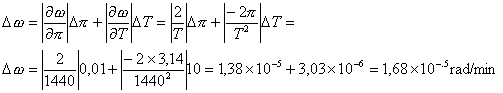Teoría de errores
1.
Objetivos.
2.
Introducción. Valor estimado y error asociado en medidas
directas.
3.
Notación: cifras significativas.
4.
Error absoluto y relativo.
5.
Errores Accidentales.
5.1.
Desviación típica.
5.2.
Error debido al aparato.
6.
Errores sistemáticos.
6.1.
Curva de calibrado.
7.
Medidas indirectas.
8.
Errores asociados a constantes físicas y números
irracionales.
9.
Ejercicios.
Muchas de las
decisiones tomadas en ingeniería se basan en resultados de
medidas experimentales, por lo tanto es muy importante expresar dichos
resultados con claridad y precisión. Los conceptos de magnitud
física, unidades y medida se han estudiado en la primera
lección de Fundamentos Físicos de la Informática
y, como complemento, en este capítulo se pretende aprender a
estimar los posibles errores en las medidas, así como la
propagación de estos errores a través de los
cálculos a los resultados, a expresar los resultados y a
analizarlos. Dado que los contenidos de esta asignatura son
fundamentalmente electricidad y magnetismo, en este curso haremos
más hincapié en las medidas de magnitudes
eléctricas.
Hay otros
parámetros para cuantificar errores y expresar resultados de las
medidas, basados en conceptos estadísticos, que no se
tratarán en esta asignatura, pero que son igualmente importantes.
1. Objetivos.
- Conocer el concepto
de error asociado a una medida.
- Aprender a estimar
el error accidental.
- Conocer el concepto
de error sistemático y su corrección mediante curvas de
calibrado.
- Saber cuantificar
los errores cometidos en las medidas indirectas.
- Conocer la
notación correcta de los resultados de las magnitudes medidas.
2. Introducción. Valor
estimado y error asociado en medidas directas.
Medir es comparar
con un patrón. Por ejemplo, si medimos la anchura del
laboratorio poniendo un pie delante de otro, podemos decir que la
anchura del laboratorio es 18 pies, siendo nuestro patrón un
pie. Ahora bien, una medida nunca puede ser exacta, es decir, siempre
cometemos un error, por lo que nuestra medida no será completa
sin la estimación del error cometido. Unas veces ese error
será debido a los instrumentos de medida, otras a nuestra propia
percepción, etc. Los errores al medir son inevitables.
En función de
la naturaleza del error podemos definir dos tipos de error:
- Errores
sistemáticos: Son debidos a
problemas en el funcionamiento de los aparatos de medida o al hecho de
que al introducir el aparato de medida en el sistema, éste se
altera y se modifica, por lo tanto, la magnitud que deseamos medir
cambia su valor. Normalmente
actúan en el mismo sentido.
- Errores accidentales: Son debidos a
causas imponderables que alteran aleatoriamente las medidas. Al
producirse aleatoriamente las medidas se distribuyen alrededor del
valor real, por lo que un tratamiento estadístico permite
estimar su valor.
Debido a la existencia de errores es imposible conocer el valor real de
la magnitud a medir. Si somos cuidadosos podemos controlar los errores
sistemáticos, en cuanto a los errores accidentales podemos
reducirlos si tomamos un conjunto de medidas y calculamos su valor
medio. Tomaremos
como valor estimado de la medida el valor medio de las distintas
medidas realizadas.
Supongamos que se
pretende medir la longitud L de una barra y se
obtienen dos conjuntos de medidas:
Grupo a : 146 cm,
146 cm, 146 cm
Grupo b : 140 cm, 152 cm, 146 cm
En ambos casos el
valor estimado es el mismo (146 cm). Sin embargo, la precisión
de las medidas no es la misma. ¿Cómo podemos diferenciar
la precisión de dos medidas? Mediante el concepto de error o
incertidumbre que definiremos más adelante.
A la hora de
expresar una medida siempre se ha de indicar el valor observado junto
con su error y la/s unidad/es correspondiente/s. Podemos decir que el
valor verdadero de la medida se encuentra con una alta probabilidad en
un intervalo cuyos límites son la estimación de la medida
más/menos el error estimado.
Medida = Valor
observado ± Error Unidad
En el
ejemplo anterior, una vez estimado el error se escribiría: L
= 146 ± 4 cm
3. Notación: cifras significativas.
A la hora de expresar el resultado de una medida junto con su error
asociado se han de observar ciertas consideraciones:
1. En primer lugar
se ha de escribir correctamente el error. Dado que su valor es
aproximado, no tiene sentido dar más allá de una cifra
significativa excepto en el caso en que al quitar la segunda cifra
significativa se modifique de forma considerable su valor. Por ello se
establece la norma en que el error se expresa con una cifra
significativa, excepto cuando esa cifra sea un 1 o cuando sea un 2
seguida de un número menor que 5, en este caso se puede expresar
con dos cifras significativas.
|
Error de V
|
Error de V
|
Error de L
|
BIEN
|
0,12 V
|
0,08 V
|
30 cm
|
MAL
|
0,1203 V
|
0,078 V
|
35 cm
|
2.En segundo lugar
se ha de escribir correctamente el valor de la medida. Tampoco tiene
sentido que la precisión del valor medido sea mayor que la
precisión de su error. El orden decimal de la última
cifra significativa de la medida y de la última cifra
significativa del error deben coincidir. Para ello se redondea el valor
de la medida, si hace falta.
|
Medida de V
|
Medida de V
|
Medida de L
|
BIEN
|
48,72 ± 0,12 V
|
4,678 ± 0,012 V
|
560 ± 10 cm
|
MAL
|
48,721 ± 0,12 V
|
4,6 ± 0,012 V
|
563 ± 10 cm
|
También
hay que tener en cuenta cuando se trabaja con número grandes o
pequeños utilizando la notación científica de
potencias de 10, que conviene escribir valor y error acompañados
de la misma potencia de 10.
BIEN
|
8,72·10-4
± 0,12·10-4 N
|
(4,678 ± 0,012)
·10-8 A |
MAL
|
872·10-6
± 0,12·10-4 N
|
4,678·10-8
± 1,2·10-10 A
|
4. Error absoluto y relativo.
El error absoluto es la diferencia
entre el valor exacto y el valor obtenido por la medida. El error
absoluto no puede ser conocido con exactitud ya que desconocemos el
valor exacto de la medida. Por eso, utilizaremos una estimación
del intervalo en el que se puede encontrar el error absoluto. A esta
estimación se la denomina error o incertidumbre,
y en este libro la
llamaremos simplemente error y se denotará mediante el
símbolo ε.
Por ejemplo, tenemos
una regla y medimos la anchura de un papel, la medida es 22,5 cm.
¿Cuál es el error absoluto cometido? Hay que estimarlo.
Si la regla está dividida en intervalos de un milímetro,
ésta puede ser una cota superior aceptable del error absoluto.
De esta forma, el valor real debería estar comprendido en un
intervalo entre 22,4 y 22,6 cm. La medida se denota entonces como 22,5
± 0,1 cm, donde 0,1 cm es el error de la medida.
El error relativo εr es el
cociente entre
el error y el valor medido. Se suele expresar en tanto por ciento. Esta
forma de expresar el error es útil a la hora de comparar la
calidad de dos medidas.
Por ejemplo, medimos
la distancia que separa Valencia de Castellón y el resultado es
75 ± 2 Km. Después, medimos la longitud del aula
resultando 8 ± 2 m. ¿Qué medida es mejor? El error
relativo de la primera es εr1 = 2/75*100 = 2,7 % y
el de la segunda es εr2 = 2/8*100 = 25 %. Por
lo tanto, la primera medida es mejor, a pesar de que el error de la
segunda medida es menor.
5. Errores Accidentales.
Como se ha dicho,
estos errores son debidos a causas imponderables que alteran
aleatoriamente las medidas, tanto al alza como a la baja. Son de
difícil evaluación, ésta se consigue a partir de
las características del sistema de medida y realizando medidas
repetitivas junto con un posterior tratamiento estadístico. De
esta forma, a partir de las medidas repetitivas se debe calcular la
desviación típica s, y a partir de las
características del aparato de medida se evaluará el
error debido al aparato, D. El error de la medida se tomará como
el máximo de estas dos cantidades
ε =
máx{s, D}
Cuando la
repetición de las medidas da prácticamente el mismo
resultado, como ocurre normalmente con los aparatos de medida
utilizados en el laboratorio de FFI, sólo se evaluará el
error D debido al aparato, pues es despreciable frente a D.
5.1. Desviación
típica.
Para obtener un buen
resultado de una medida, minimizando el efecto de los errores
accidentales, es conveniente repetir la medida varias veces. El valor
medio será el que tomaremos como resultado de la medida, ya que
probablemente se acerque más al valor real. Cuantas más
repeticiones de la medida se efectúen, mejor será en
general el valor medio obtenido, pero más tiempo y esfuerzo se
habrá dedicado a la medida. Normalmente a partir de un cierto
número de repeticiones no vale la pena continuar.
¿Cuál es el número óptimo de repeticiones?
Para decidirlo hay que realizar tres medidas iniciales. A partir de
estas medidas se calcula la dispersión D. La
dispersión de una medida es la diferencia entre el valor
máximo y el mínimo obtenidos, dividido entre el valor
medio, expresado en tanto por cien:
Si el valor de la
dispersión es mayor del 2% es necesario realizar más
medidas, según la tabla siguiente
|
D < 2 %
|
con tres medidas es
suficiente
|
|
2 % < D
< 8 %
|
realizar un total de seis
medidas
|
|
8 % < D
< 12 %
|
realizar un total de quince
medidas
|
|
D > 12 %
|
mínimo 50 medidas y
tratamiento estadístico
|
Si se ha
repetido la medida N veces calcularemos
la desviación típica mediante la expresión:
Donde 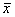 es el valor medio, xi
es el valor de cada
medida y N es el numero de
medidas.
es el valor medio, xi
es el valor de cada
medida y N es el numero de
medidas.
5.2. Error debido al aparato.
Existen diferencias
entre la forma de evaluar los errores debidos a los aparatos. Se ha de
distinguir entre aparatos analógicos y digitales. Pueden
estimarse estos errores a partir de las características
técnicas de los aparatos, como se verá a
continuación. Estas características aparecen en las hojas
de especificaciones del aparato, o vienen indicadas en el propio
aparato. En la página siguiente se muestra como ejemplo la hoja
de especificaciones del multímetro digital Demestres 3801A.
Aparatos
digitales.
El error accidental
que se comete en un aparato digital es la suma del error de
precisión y el error de lectura.

Error de
precisión: Es un porcentaje
del valor leído en pantalla. Ejemplo:
Error
de
precisión: 1%
Medida: 4,56 V
Error de
precisión: 4,56 * 1/100 = 0,05 V
Error de lectura: La salida en
pantalla se realiza con un número limitado de dígitos por
lo que, aunque el aparato pueda medir con mayor precisión,
sólo nos podrá mostrar una medida limitada al
número de dígitos de que dispone. El error de lectura
equivale a N unidades del último dígito. Ejemplo:
Error
de lectura: 3d
(tres unidades)
Medida: 4,56 V
Error de lectura:
0,01 · 3 = 0,03 V
El error debido al
aparato
será la suma D = 0,05 + 0,03 = 0,08 V

Un ejemplo: Al medir
una tensión en un circuito de corriente continua con un
multímetro cuyas características aparecen en la figura
inferior, podríamos observar que el error de precisión es
el 0,5% de la medida en cualquier escala y el error de lectura es de un
dígito, lo que equivale a 0,01V si estamos en la escala de 20V y
por tanto en la pantalla aparecen dos decimales.
Aparatos
analógicos.
El error debido a un
aparato analógico es la suma del error de clase y el error de
lectura. El error de clase viene indicado en las especificaciones del
aparato, normalmente mediante la palabra CLASE o el vocablo
inglés CLASS.
Error de clase: Es
un porcentaje
del fondo de escala. El fondo de escala es el máximo valor
medible del aparato. Ejemplo:
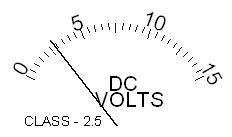
Error de clase: 2,5
Medida: 3 V
Fondo de escala: 15 V
Error de clase:
15·2,5/100 = 0,375 V
Observa que el error
de clase es independiente del valor obtenido en la medida.
Error de lectura: Es el error
cometido en la lectura de las divisiones de la escala. Lo evalúa
el operador. Esa cantidad varía según la persona que
realice la medida y se expresa como la porción de la
división mínima que el operador es capaz de diferenciar.
Ejemplo:
Error de lectura:
1/2 división
Voltios/división: 0,5 V
Error de lectura:
0,5·1/2 = 0,25 V
El
error debido al
aparato
será la suma D = 0,375 + 0,25 = 0,6 V donde se ha
efectuado ya el redondeo correcto.
Otros
casos.
En ocasiones se
trabaja con aparatos de medida sencillos, como un reloj (digital o
analógico) o una regla, y no se dispone de sus especificaciones
técnicas. En ese caso se evaluará solamente el error de
lectura, tomando 1 dígito para los aparatos digitales y la
porción de la división mínima que el operador es
capaz de diferenciar para los analógicos.
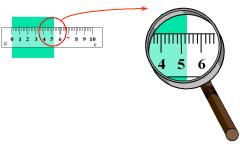
Ejemplo:
Valor observado = 5,2
Error de lectura
= 0,2
Unidad = cm
Resultado L = 5,2 ± 0,2
cm
6. Errores
sistemáticos.
Los errores
sistemáticos son debidos a defectos en los aparatos de medida o
al método de trabajo. Normalmente actúan en el mismo
sentido, no son aleatorios, siguiendo unas leyes físicas
determinadas, de tal forma que en ocasiones se podrán calcular y
compensar matemáticamente tras la medida. Un ejemplo
podría ser el de una regla graduada pero dilatada por el calor,
esa regla daría como resultado longitudes siempre menores que
las reales. Otro ejemplo sería la medida de la corriente
eléctrica que circula por un conductor mediante un
amperímetro. Al introducir el amperímetro en el circuito
éste se modifica, de manera que la corriente medida no es
exactamente igual a la corriente que circulaba antes de colocar el
amperímetro. En este ejemplo el propio aparato de medida
modifica el resultado.
Los métodos
para corregir estos errores sistemáticos son variados. En el
caso de la regla dilatada habría que confeccionar una curva de
calibrado, tal y como se describe en el próximo apartado. En el
segundo caso bastaría con averiguar la resistencia del
amperímetro y calcular con ella el error sistemático
producido mediante el análisis del circuito.
6.1. Curva de
calibrado.
Una forma de
corregir los errores sistemáticos es realizando una curva de
calibrado, que es una gráfica que relaciona los valores medidos
con los valores reales. Para ello hay que disponer de algún
patrón o magnitud cuyo valor es conocido. En el ejemplo de la
regla dilatada bastaría con medir con ella uno o más
patrones de longitudes conocidas para trazar una recta (o curva) de
calibrado.
Una vez se dispone
de la curva de calibrado, cualquier medida realizada con el sistema se
puede transformar en un resultado libre del error sistemático
sin más que consultar la curva de calibrado que relaciona los
valores medidos con los reales.
Ejemplo: Durante un
largo
viaje de vacaciones se observa que las medidas del
cuentakilómetros de nuestro coche no coinciden exactamente con
las señales kilométricas de las carreteras. Parece que el
cuentakilómetros siempre marca una distancia mayor, existiendo
un error sistemático en las medidas. Confiando en la exactitud
de la señalización de la carretera, se decide realizar
una calibración del cuentakilómetros, anotando su lectura
cada vez que se alcanza una de las señales. El resultado aparece
en la tabla siguiente.
Señalización
(km)
|
Cuentakilómetros (km)
|
|
1,00
|
1,0
|
|
5,00
|
5,3
|
|
10,00
|
10,5
|
|
25,00
|
26,2
|
La curva de
calibrado para nuestro cuentakilómetros se muestra en la
siguiente figura.
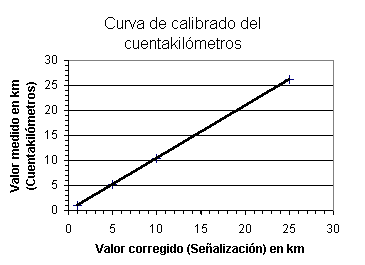
Cuando han
transcurrido 20 km según nuestro cuentakilómetros, puede
comprobarse en la curva de calibrado que en realidad se han recorrido
19 km. Éste valor es pues el resultado de la medida una vez
corregido el error sistemático del cuentakilómetros
mediante la curva de calibración.
7. Medidas indirectas.
En muchas ocasiones
no podemos medir directamente una magnitud y obtenemos su valor
mediante un cálculo, después de haber medido otras
magnitudes relacionadas con aquella. Esto se hace por medio de un
expresión analítica o fórmula. Los valores
obtenidos de las medidas previas al cálculo están
afectados por un error de medida y estos errores se propagan en las
operaciones de cálculo.
Supongamos que la
magnitud F se calcula en
función de las magnitudes x, y, z que al
medirlas
vienen afectadas por errores Δx, Δy, Δz.
¿Cómo
se calcula el error de la medida indirecta F?
El error de una
medida indirecta se calcula
Ejemplo:
Medida del
área de un rectángulo a partir de la medida de la
longitud de sus lados a y b

a = 5,3 ± 0,1
cm b = 4,0 ± 0,1
cm
S= a b = 21,2 cm2
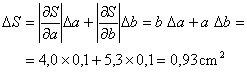 S = 21,2 ± 0,9
cm2
S = 21,2 ± 0,9
cm2
8. Errores asociados
a constantes
físicas y números irracionales.
Cuando al realizar
una medida indirecta incluimos una constante física o un numero
irracional, sólo utilizamos un número finito de
decimales. Esto introduce un error que puede ser importante a la hora
de calcular el error de la medida indirecta. Así pues, hay que
asignar un error a las distintas constantes físicas o
números irracionales que aparezcan en las leyes físicas.
El error asociado será de una unidad de la última cifra
decimal utilizada.
Por ejemplo, al
utilizar el valor de p con distintos número de cifras, los
errores asociados son
3,14
± 0,01
3,1416 ±
0,0001
3,1 ± 0,1
Al aplicar la
expresión del cálculo de errores de magnitudes indirectas
hay que considerar los números irracionales como variables
respecto de las cuales hay que derivar la magnitud en cuestión.
Ejemplo:
¿Cuál es la velocidad angular de rotación de la
tierra?
Datos: El tiempo que
tarda en dar una revolución es T = 1440 ± 1 min
Solución: La
velocidad angular es ω= dφ/dt = 2π / T
Tomando π = 3,14
entoces ω = 2·3,14 /
1440 = 4,361*10-3 rad/min
En unidades del SI ω
= (4,361*10-3) / 60 = 7,268*10-5 rad/s
El error asociado a
esta medida es:
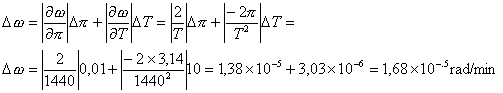 En unidades del SI
Δω = 1,68* 10-5 / 60
= 0,028*10-5 rad/s
El
resultado es ω =
7,27*10-5 ± 0,03*10-5 rad/s
En unidades del SI
Δω = 1,68* 10-5 / 60
= 0,028*10-5 rad/s
El
resultado es ω =
7,27*10-5 ± 0,03*10-5 rad/s
Sin
embargo, si se
utilizan los valores de las constantes y números irracionales
suministrados por una calculadora u ordenador, normalmente tienen
tantas cifras decimales que el error que introducen es despreciable.
9. Ejercicios.
1. Calcula la
superficie de una moneda de 1€.
Para
ello mide el diámetro de la moneda y anota el resultado.
Comparte tu resultado con los resultados de otros compañeros y
completa la tabla siguiente:
D1
|
D2
|
D3
|
D4
|
D5
|
D6
|
D7
|
D8
|
D9
|
D10
|
|
|
|
|
|
|
|
|
|
|
Completa las tablas siguientes:
|
Diámetro
de la moneda (media)
|
|
|
Expresión
correcta de la superficie
|
|
2. ¿Están
correctamente expresadas las siguientes medidas? Razona tu respuesta.
48,3 ± 0,2874
V
3460 ± 26,67 V
48,3245 ± 0,3 V
3455,656 ± 30 V
48,3 ± 0,3 V
3. Deduce el error
absoluto de la densidad (ρ =M/V) en función
de los errores de la masa y el volumen.
4. Deduce el error
absoluto de la magnitud Z = X-Y, si X e Y
vienen afectados por
sendos errores ΔX y ΔY.
5. Por una resistencia
de valor 110±11 Ω circula una intensidad de corriente I,
que medida con un
amperímetro digital, tiene un valor de 1,78 A. Las
especificaciones del amperímetro señalan que su
precisión es (1 % + 1d). Calcula la
potencia disipada por la resistencia, con su error (P=R I2).
6. La capacidad de un
condensador es C = 6,2 ± 0,2 μF.
Este condensador se carga con una cierta carga Q. Se mide la
d.d.p. entre placas con un
voltímetro digital y la lectura es la que se muestra en la
figura. La precisión del voltímetro es 2% y 1
dígito
¿Cuál es el valor de la carga Q, con su error Δ
Q ? ( Q=C V)

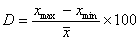
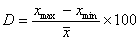
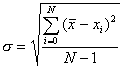
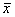 es el valor medio, xi
es el valor de cada
medida y N es el numero de
medidas.
es el valor medio, xi
es el valor de cada
medida y N es el numero de
medidas.